Shamir's Secret Sharing Scheme en PHP
Publié le 24 février 2021
Ssss... Ce n'est pas le son d'un serpent mais les initiales de Shamir's Secret Sharing Scheme. Avant d'expliquer ce dont il s'agit, laissez-moi contextualiser.
Il y a un peu plus d'un an j'ai travaillé avec Kévin Dunglas sur API Platform et à ce moment-là, il y avait des modifications à effectuer sur les conteneurs de la distribution. Mercure.rocks venait d'arriver et la restructuration nécessitait d'avoir du HTTP/2 + SSL pour bénéficier des capacités de HTTP/2 PUSH. Seulement, il y avait des problématiques de génération de certificats. Je savais comment générer les certificats mais je suis devenu curieux. J'ai voulu comprendre ce qu'il se passe vraiment lorsqu'un certificat est émis. Quelle est la mécanique derrière HTTPS ? Comment sont utilisés les certificats, et comment sont sécurisés les échanges ?
J'ai donc fait mes devoirs, et autant que d'autres en profitent. J'ai écrit une conférence dédiée à RSA, ainsi qu'une suite d'articles disponible en 3 parties : partie 1, partie 2 et partie 3. Cette suite d'articles a ensuite donné lieu à une conférence (pour ceux qui n'ont pas le courage de lire) :
Dans un autre registre d'opportunité, j'ai eu la chance de participer à un hackathon Symfony / API Platform organisé par la Commission Européenne durant lequel un nouveau composant Symfony est né. Composant... une nouvelle fonctionnalité plutôt, parce que techniquement ce n'est pas un composant indépendant. Mais je vais continuer de dire composant quand même, c'est le composant « secrets ».
Il permet de chiffrer vos secrets (comme un mot de passe de base de données), et il est d'ailleurs très pratique lorsque vous manquez de confiance envers votre hébergeur, ou tout simplement parce que vous êtes soucieux de la sécurité et qu'il n'est pas possible pour vous d'utiliser de variable d'environnement sur votre serveur.
Il utilise une librairie C (libsodium) à travers une API dédiée en PHP et il se trouve que les méthodes de chiffrements utilisées par libsodium pour le composant « secrets » sont les mêmes algorithmes que ceux utilisées dans RSA ! J'avais donc la possibilité de promouvoir cette fonctionnalité tout en expliquant les mécaniques sous-jacentes. Chose qui m'a été offerte lors du Symfony World 2020 où j'ai pu confronter mes connaissances, lors de différents échanges avec d'autres contributeurs de Symfony.
L'un d'eux (coucou Jérémy !) m'a alors fait la réflexion suivante : "avant il y avait des secrets dans un fichier connu que du serveur. Maintenant, il y a des secrets chiffrés dans un fichier connu de tous, mais déchiffrable uniquement avec la clé connue que du serveur. Dans les 2 cas, que se passe-t-il si je n'ai pas confiance en mes fournisseurs ? Que ce soit un serveur classique, ou des conteneurs dans le cloud, il faut que la clé soit déposée quelque part. Je n'ai pas de solution parfaite encore pour protéger cette clé...". C'est alors que je me suis souvenu avoir vu une vidéo d'un mathématicien : Matt Parker. Dans cette vidéo il explique un principe mathématique permettant de diviser un secret en une multitude de morceaux, trois, cinq, douze. Mais n'ayant besoin que d'un certain minimum de morceaux pour reconstruire l'intégralité du secret.
Je me suis demandé si ça ne pouvait pas être une solution. Et il se trouve que oui. Par ailleurs, l'excellent VaultProject.io de HashiCorp utilise cette même technique pour protéger les clés. Je me suis dit que ce serait top si ça existait en PHP ! Et puis j'ai oublié de chercher dans Google. Je suis allé voir des revues mathématiques et j'ai rien compris. Je suis allé lire des pages Wikipédia et j'ai rien compris. J’ai ouvert des pages, et autres articles de blogs vulgarisateurs, j'ai compris un peu. J'ai revu la vidéo de Matt Parker, je l'ai un peu plus comprise, puis j'ai réouvert Wikipédia que j'ai compris et enfin, j'ai réouvert les revues mathématiques et je n’ai toujours pas compris. Alors pourquoi ça marche ?
Prenons mon mot de passe de session d'ordinateur : « peanuts! » Je vais envoyer des pièces incomplètes à des tiers :
- p _ _ nu _ _ _
- _ e _ _ _ t _ !
- p _ a _ _ _ s _
En combinant les 3 morceaux, je peux reconstituer la valeur d'origine mais avec seulement 2, il va me manquer des éléments.
Disons que je crée plus de variations, je peux alors imaginer qu'il y ait un certain nombre de lettres communes ainsi qu'un certain nombre de lettres absentes dans chaque variation. Cette valeur que j'aurais décidée au préalable me permet de contrôler le nombre de variations minimum dont j'ai besoin pour retrouver la valeur d'origine. Moins j'ai d'intersections entre les variations, plus j'ai besoin de morceaux, pour recomposer la valeur. Je peux ainsi donner mon mot de passe, sans qu'il ne soit mis en danger, à moins que les tiers ne décident de se concerter pour le décoder !
Sur le principe énoncé précédemment voilà comment les mathématiques sont appliquées. Nous allons transformer notre chaîne de caractères à subdiviser, en valeur numérique. Pour l'exemple, disons que mon mot de passe nous donne la valeur 42. Nous allons créer une fonction, dont la première entrée est notre valeur numérique : 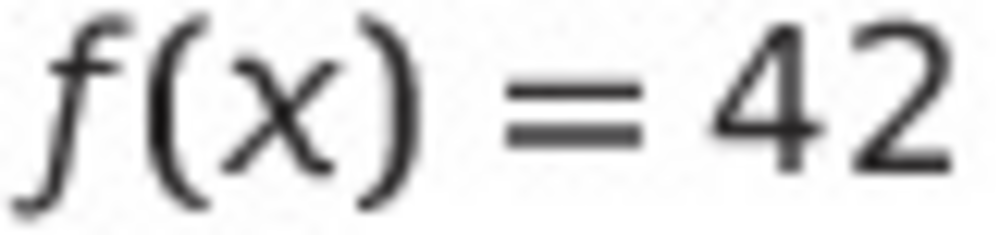 .
.
Sous cette forme, ça ne fait pas grand-chose. Nous allons y ajouter des valeurs. Une de moins que de "morceaux/parts" désirés pour pouvoir plus tard reconstruire la valeur. Si je m'impose de ne pouvoir reconstituer le secret qu'avec au moins k = 3 "morceaux", la fonction devient alors : 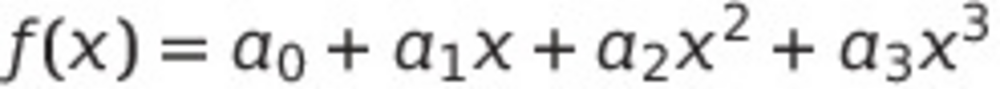 .
.
De manière générale, la formule est : 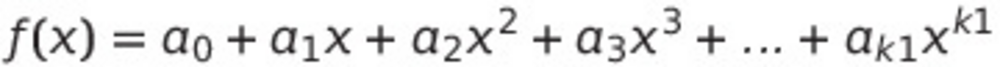 (a0 étant notre secret). Ce type de fonction porte un nom : polynomiale. Il faut sélectionner pour chaque "degré" (le nom des valeurs) un nombre entier positif sélectionné au hasard. Par exemple, prenons des valeurs simples comme 3 puis 5 :
(a0 étant notre secret). Ce type de fonction porte un nom : polynomiale. Il faut sélectionner pour chaque "degré" (le nom des valeurs) un nombre entier positif sélectionné au hasard. Par exemple, prenons des valeurs simples comme 3 puis 5 : 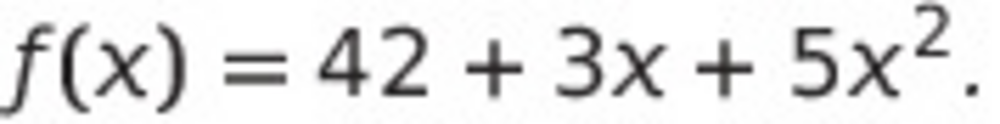
Que se passe-t-il si je passe 0 à notre fonction ? Vous l'avez tout de suite compris, les multiplications et les montées en puissance vont résulter à 0. Nous obtiendrons la seule valeur importante, notre secret. C'est l'opération que l'on souhaite effectuer à la fin, avoir été capable de reconstruire cette formule, pour pouvoir retrouver notre secret. Sur un graphe orthonormé, la formule résultera en une courbe avec laquelle lorsque l’on donne x = 0, y nous donnera la valeur du secret.
Partant de ce principe, nous allons donc aller chercher au moins 3 points sur cette courbe. Prenons 4 valeurs qui seront les x. 18, 27, 31, 35. La formule nous donne les y suivants : 1716, 3768, 4940, 6272. Soit les points (18, 1716), (27, 3768), (31, 4940) et (35, 6272).
Et maintenant ? Et bien, il est temps d'envoyer un point à chaque service/serveur/client de confiance ainsi que la valeur k, nécessaire pour la reconstruction.
Nous possédons un point. C'est bien, mais ça ne nous indique rien.
Mais si nous connaissons le nombre d'entrées nécessaire pour la formule, alors en possédant autant de points dans l'espace il est possible de "deviner" la formule. Pour le faire, il faut utiliser l'interpolation polynomiale de Lagrange. Je vous passe la formule, mais si vous êtes curieux, elle est ici. Une fois reconstruite, vous aurez compris qu'en donnant la valeur 0 à cette formule, nous devrions retomber sur notre secret !
Il reste un détail crucial à couvrir. Sans connaitre k, il n'est pas vraiment possible de reconstruire la formule, mais, si un attaquant arrive à se procurer un nombre suffisamment grand de points générés. Alors il réduit la marge d'erreur et peut lui aussi finir par deviner la courbe. S’il obtient k, alors des méthodes mathématiques lui permettent de déduire certaines valeurs, les unes après les autres.
Ceci est possible parce que nos points représentent exactement des valeurs supérieures à notre secret.
Pour contourner ce problème, il faudra ajouter une opération modulo à notre formule pour brouiller les pistes. Sans la valeur des points, ni de k, ni du modulo, impossible de reconstruire la formule ni de deviner les emplacements réels. Pour bien faire la valeur du modulo sera un nombre premier bien entendu.
Let's make baby steps with PHP. Créez le nécessaire pour constituer la formule.
<?php
// split into N shares here 3 for example it mean I need a polynomial function of degree 2. (k-1)
$k = $minShares;
$m = $modulo; // including our secret, we need 2 more numbers at random to plot our function.
// they are coefficient, no real needs to be high.
$numbers = array_map(static function () {
return (string)random_int(0, 99);
}, array_fill(0, $k - 1, null));
$polynomial = new Polynomial([...$numbers, $secret], $m);// let generate N points to dispatch
$points = array_map(static function () use ($polynomial) {
$rand = random_int(0, 100);
return ["$rand", $polynomial("$rand"), $polynomial->quotient];
}, array_fill(0, $maxShares, null));
return $points;L'objet Polynomial est issu du travail de Mark Rogoyski que j'ai revu pour mes besoins. C'est lui qui porte la responsabilité de créer la fonction et de l'exécuter. Avec ces points, il faut à présent être capable de reconstituer la fonction.
<?php
$lp = LagrangePolynomial::interpolate($points, $m);
$secret = $lp('0', false);L'objet LagrangePolynomial est lui aussi issu du travail de Mark Rogoyski, également revu pour mes besoins. Premier essai après quelques heures, j'obtiens les points, et j'obtiens de nouveau le secret !
Proof Of Concept réussi et du premier coup ! Attendez… c'est louche. J'ai tenté les mêmes valeurs que celles de mon exemple (42). Dans un cas réel, j'aurais plutôt une clé probablement générée par LibSodium.
<?php
$secretKey = SodiumHelper::generateKey(); // this will be stored in shares.
$nonce = SodiumHelper::generateNonce(); // this could be part of your app configuration$secret = 'Sensitive information';
var_dump("secret : $secret");// symmetric key encryption with padded message to hide it's length. This does not matter, it's for show !
$encryptedMessage = SodiumHelper::encrypt($secret, $secretKey, $nonce);
$number = gmp_import($encryptedMessage);
$valueToPlot = gmp_strval($number);et j'obtiens plutôt des valeurs comme 1472502186037957747441234705645302953943147992477563238054054428338355254101. Un peu plus important que 42. Voyons si les maths tiennent la route. NON Évidemment, le résultat explose littéralement. Après quelques coups de débogage, je constate que la génération des points est valide. C'est la suite qui se corse. En effet, l'interpolation polynomiale de Lagrange joue avec des additions (ça va), des multiplications (ça va), des divisions (oula !) sur de grandes valeurs... Et si vous n'avez pas encore vu l'excellente conférence de Benoit Jacquemont sur le sujet : allez-y, il y a de grandes chances que je sois dans cette situation !
Je ne me décourage pas j'essaie de trouver les raisons des erreurs. Même s’il y a des approximations, je dois pouvoir m'en sortir, je ne suis pas le premier à faire des calculs sur de grands nombres. Et ce n'est pas comme si je manipulais des flottants dès le départ ! Les approximations ne devraient pas être un problème dans ma situation.
Je remplace tous les calculs mathématiques par gmp car il semble tout indiqué, jusqu'au moment où j'arrive sur les opérations modulo. J'ai besoin de récupérer le quotient de l'opération, or rien ne le permet sans réeffectuer les calculs derrière. Qu'à cela ne tienne, allons-y. Manque de bol, j'ai de nouveau des soucis d'approximation.
Je remplace tous les calculs mathématiques par bcmath, l'autre solution qui semble aussi adaptée. Bon là, il y a un peu plus de travail, puisque bcmath manipule des strings. Je vais devoir modifier un peu plus que juste les opérations. À cœur vaillant, rien d'impossible, ça prendra juste un peu de temps. Rebelote. Problèmes d'approximation... C'est vraiment, vraiment pas cool PHP pour les maths. Je m'y prends peut-être mal, mais je suis alors pris d'une frénésie, et me lance même dans la ré-écriture du code en R ! Mais il est tard... je mets en pause le dev.
Je reviens sur mes pas. Clairement en PHP, le plus à même de faire le job, c'est bcmath. Et je suis sûr que d'autres ont rencontré le problème, alors je décide d'aller à la boîte à outils, pour comprendre où l'approximation démarre. En PHP, l’approximation vient des Float et Double. Mais elle peut l’être moins grâce à l'écriture scientifique ! Et tant que je manipule des doubles ET l'écriture scientifique, sur le papier, je ne dois pas perdre en précision. Mais, Ô grand Mais, lorsque cette écriture scientifique est utilisée, particulièrement lors de l'usage de modulo, la chaîne numérique obtenue, est imprécise ! Caster en float, utiliser number_format ou utiliser sprintf d'un double en écriture scientifique, n'est pas précis sur des valeurs si grandes. Et croyez-moi j'ai écumé les discussions sur le sujet.
Il faut que je trouve une parade à l'écriture scientifique. Après des heures de recherche, je trouve une librairie qui apporte sa méthode de conversion de l'écriture scientifique ainsi que des ajustements des méthodes de bcmath. Exactement ce dont j'avais besoin (ouf pas besoin de l'écrire), si tant est qu'elle fonctionne et corrige mes problèmes d'approximation. Je l'importe et remplace... Je n'ose pas regarder la sortie du terminal...
Ça a marché ! Et me voici avec un prototype qui fonctionne !
Le dépôt est ici, je partage le code aux collègues, c'est un réfllexe, j'ai des encouragements, c'est cool. On me demande si ça n'existe pas déjà, c'est aussi un réflexe. Je réponds que non, je ne me serais pas cassé la tête sinon... c'est pas cool.
Pas cool, parce que plus tard, je réalise que je n'ai jamais tapé les mots clés « shamir, secret, sharing, php » dans un moteur de recherche... J'ai foncé tête baissée. Oh je m'en veux. Parce qu'il y a ça et ça m'a pas l'air mal du tout : ce que j'aime c'est que le soin a été pris de couvrir les aspects critiques de la sécurité mathématique, avec l'application d'un modulo sur les résultats pour masquer la longueur du secret. C'est top. En prime, la librairie hash le résultat des morceaux pour n'avoir qu'une chaîne simple à stocker, tandis que pour l'instant mon code renvoie un tableau, mais ce ne serait pas très difficile à implémenter. Enfin, il y a un détail qui me fait un peu peur parce que je manque de connaissances mathématiques, c'est que sa librairie impose le choix du nombre premier utilisé dans l'exécution du modulo. L'intérêt de ce modulo est de brouiller les pistes, mais si en connaissant la librairie, on connait la valeur du modulo, je pense que cela perd complètement de son usage (mais je peux me tromper), tandis qu'au contraire, dans ma librairie, je demande à l'utilisateur de donner cette valeur, pour qu'elle puisse être différente d'une installation à une autre. Un peu plus de contraintes, pour un peu plus de sécurité. C'est à pondérer, et surtout à confirmer par quelqu'un de plus expert que moi.
- Le plus évident puisque c'est pour ça que j'ai travaillé dessus : diviser et partager des clés privées. Par exemple, la clé utilisée pour les secrets de Symfony, ou encore la clé privée pour les token JWT (qui en passant mérite une plus grande attention).
- L'Authentication As Service.
- L'amélioration de la sécurité d'ouverture de salle par RFID.
Laissez libre cours à votre imagination, je suis sûr que vous trouverez d'autres usages !
C'est un concept qui fonctionne, mais qui est encore un concept ici, je manque de validation de la part de chercheurs en sécurité. Mais je serai ravi d'en discuter ! Merci de m'avoir lu et à bientôt !



